¿Podemos decir que existen ecuaciones bonitas en matemáticas? Los científicos dicen que sí
Según los matemáticos, se han revelado las ecuaciones más bellas, estimulantes y convincentes. ¡Descubre aquí algunas de ellas!
Los matemáticos consideran las ecuaciones como arte. Así como a muchos les conmueve un cuadro o una pieza musical, para quienes aprecian y comprenden las matemáticas, las expresiones de números, variables, operaciones y relaciones entre cantidades pueden resultar igualmente atractivas.
Al igual que ocurre con la belleza artística, "la belleza matemática está en el ojo del espectador", y un matemático puede valorar ecuaciones simples y concisas, mientras que otro puede preferir lo contrario.
De este modo, tanto las ecuaciones antiguas como las contemporáneas son admiradas por su inteligencia, poder y capacidad.
Ecuación diferencial de Loewner
La ecuación diferencial de Loewner, fue introducida por Charles Loewner en 1923 y describe la evolución temporal de una familia de funciones conformes (que preservan los ángulos) definidas en subconjuntos del plano complejo.
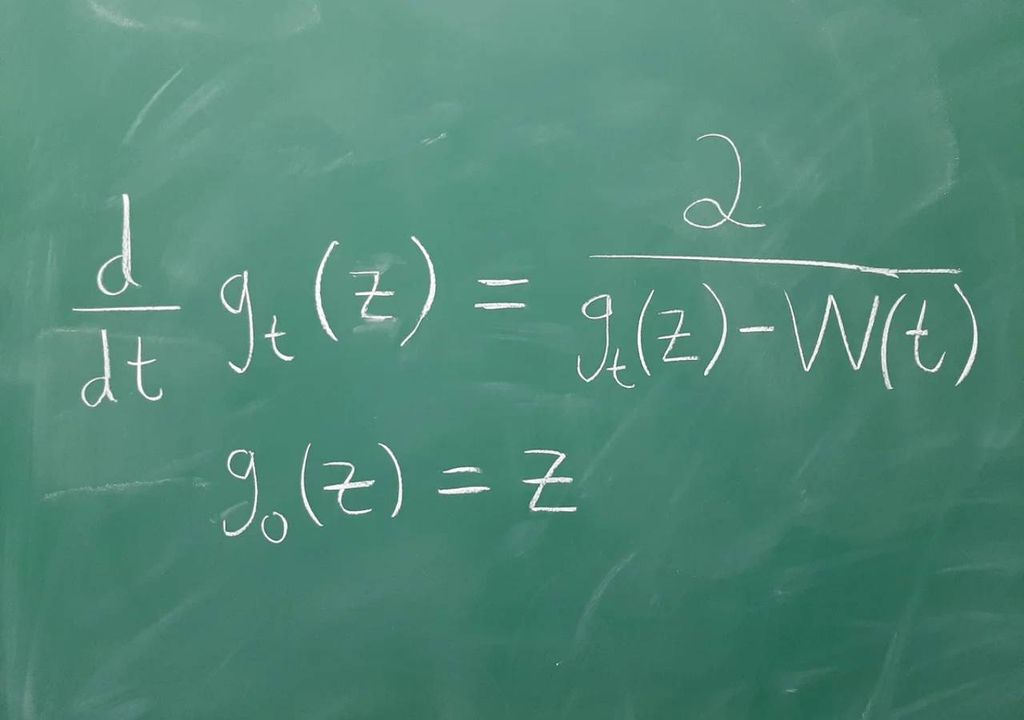
Casi 80 años después, en 1999, Oded Schramm descubrió que la solución de la ecuación de Loewner tiene simetrías especiales cuando la función impulsora se considera un movimiento browniano, una función aleatoria que es un objeto central de estudio en la teoría de la probabilidad.
Basado en el descubrimiento de Schramm, se demostró que la solución de la ecuación de Loewner para esta elección de función impulsora, llamada evolución de Schramm-Loewner, describe el comportamiento a gran escala de varios modelos críticos en mecánica estadística bidimensional.
Así, esta ecuación revolucionó el estudio matemático de la mecánica estadística y condujo a algunos de los descubrimientos matemáticos más interesantes de las últimas dos décadas, según Ewain Gwynne de la Universidad de Chicago.
Ecuación de Gauss-Bonnet
La fórmula de Gauss-Bonnet es una hermosa ecuación en geometría diferencial que establece la igualdad de la curvatura gaussiana integral sobre una superficie y una constante multiplicada por la característica de Euler de la superficie.
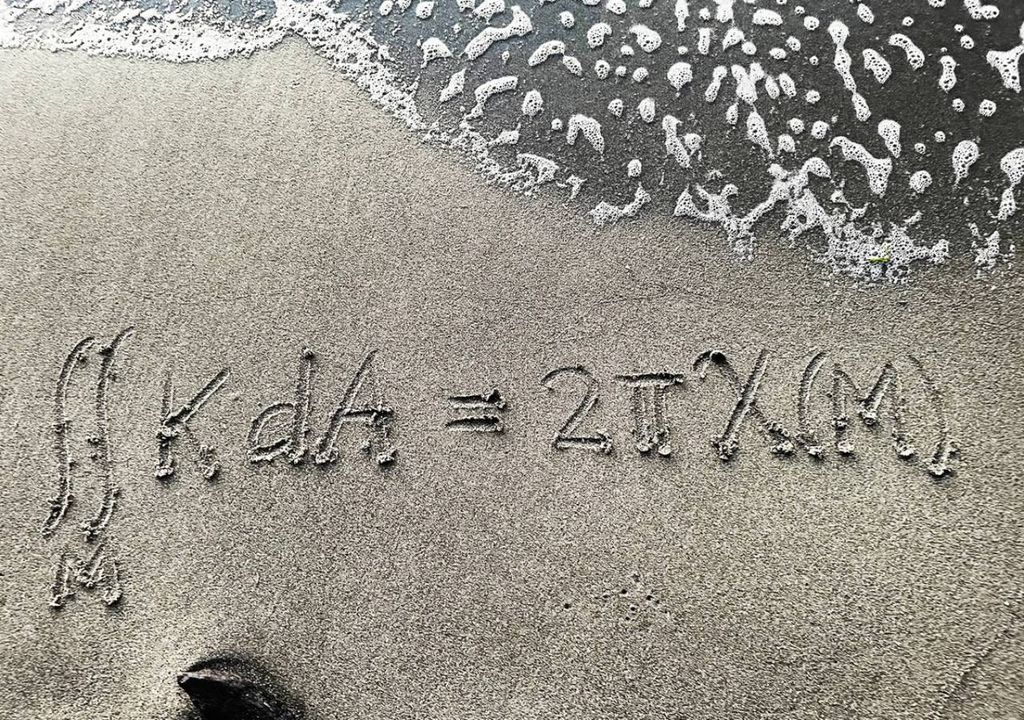
La ecuación destaca porque relaciona dos cantidades muy diferentes: la curvatura de la superficie, por un lado, y la topología de la superficie, por el otro.
La característica de Euler es un invariante topológico global de la superficie que describe la estructura topológica de la superficie independientemente de la forma en que esté curvada.
Según Ailana Fraser de la Universidad de Columbia Británica, algunos de los aspectos más bellos de esta ecuación son la simplicidad de su expresión.
Una suma infinita
Esta importante y aparentemente básica función, que tiene que ver con sumar y contar, es hermosa y quizás inesperadamente compleja.
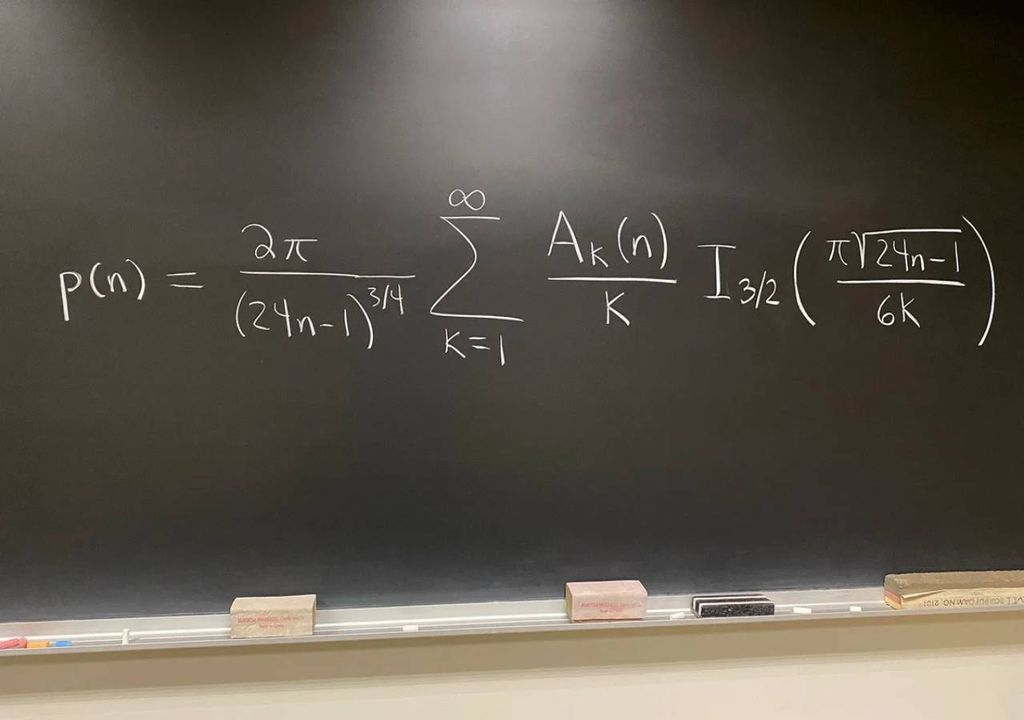
El lado derecho de esta ecuación es una fórmula exacta gracias al trabajo de 1937 de Hans Rademacher.
Algunos pueden considerar el (gran) lado derecho, una suma infinita que incluye sumas de números complejos (imaginarios) (Ak(n)), potencias fraccionarias (3/4 y la raíz cuadrada), el número trascendental pi, entre otros, como lo contrario de bello o como intimidante - especialmente porque sustituye al (visualmente pequeño) lado izquierdo que hasta un niño puede entender.
Amanda Folsom de Amherst College dice que es hermoso que la suma infinita que aquí aparece converge, lo que significa que suma algo finito, un número real que dice algo importante, y que no se sigue acumulando.